Table Of Content
Recall that Schnall and her colleagues were interested in the harshness of people’s moral judgments. To measure this construct, they presented their participants with seven different scenarios describing morally questionable behaviors and asked them to rate the moral acceptability of each one. Although the researchers could have treated each of the seven ratings as a separate dependent variable, these researchers combined them into a single dependent variable by computing their mean. When an experiment includes multiple dependent variables, there is again a possibility of carryover effects.
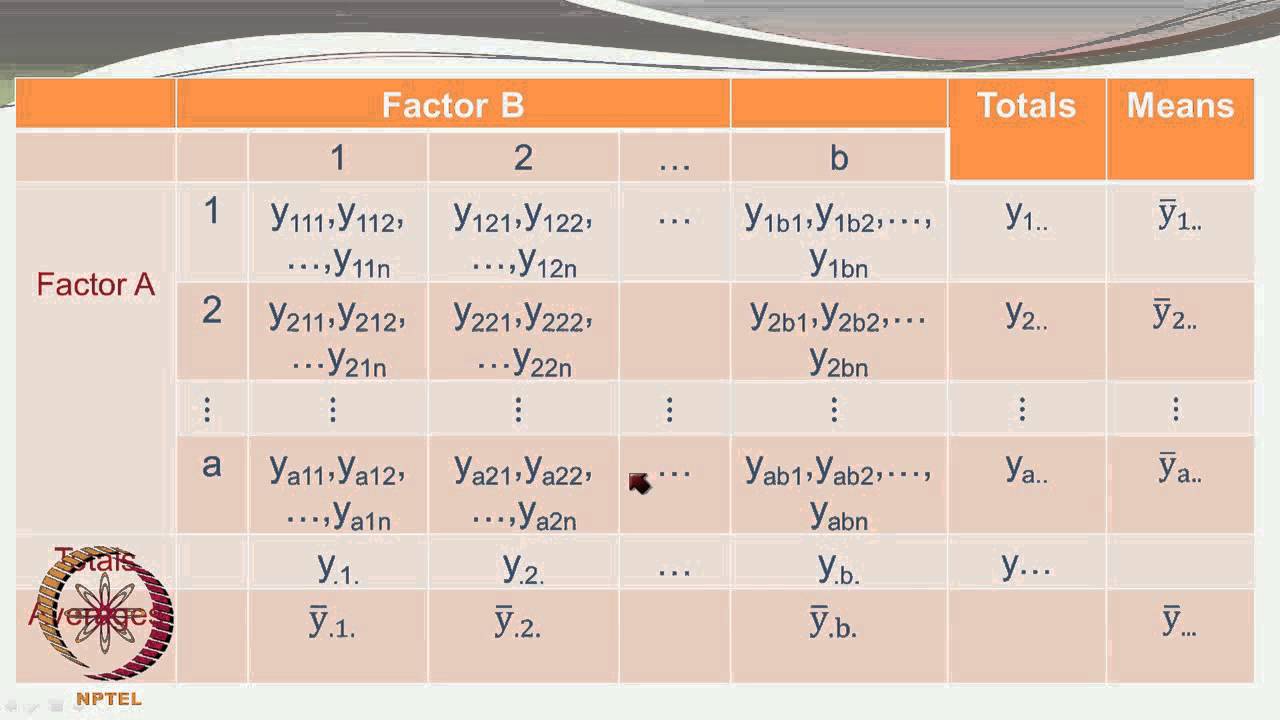
Setting Up a Factorial Experiment
For example, it is possible that measuring participants’ moods before measuring their perceived health could affect their perceived health or that measuring their perceived health before their moods could affect their moods. So the order in which multiple dependent variables are measured becomes an issue. One approach is to measure them in the same order for all participants—usually with the most important one first so that it cannot be affected by measuring the others. Another approach is to counterbalance, or systematically vary, the order in which the dependent variables are measured. It would seem almost wasteful to measure a single dependent variable. Even if you are primarily interested in the relationship between an independent variable and one primary dependent variable, there are usually several more questions that you can answer easily by including multiple dependent variables.
Types of Factorial Designs
However, there are risks…if there is only one observation at each corner, there is a high chance of an unusual response observation spoiling the results. There would be no way to check if this was the case and thus it could distort the results fairly significantly. You have to remind yourself that these are not the definitive experiments but simply just screening experiments to determine which factors are important. The analysis of variance summary table results show us that the main effects overall are significant.
V. Chapter 5: Experimental Research
However, factorial experiments do not permit strong inferences about how well a particular grouping of components (occurring as levels of different factors) will work as an integrated treatment as compared to a control. After all, only a small portion of a sample in a factorial experiment will get a particular set of components (e.g., in the design depicted in Table 1 only 1/32 of the N will get a particular combination of components). It is also possible to manipulate one independent variable between subjects and another within subjects. First, non-manipulated independent variables are usually participant background variables (self-esteem, gender, and so on), and as such, they are by definition between-subjects factors.

Assigning Participants to Conditions
In a factorial experiment, the decision to take the between-subjects or within-subjects approach must be made separately for each independent variable. In a between-subjects factorial design, all of the independent variables are manipulated between subjects. For example, all participants could be tested either while using a cell phone or while not using a cell phone and either during the day or during the night. This would mean that each participant would be tested in one and only one condition.
Two-level factorial experiments
Experimental design and response surface method in geothermal energy: A comprehensive study in probabilistic ... - ScienceDirect.com
Experimental design and response surface method in geothermal energy: A comprehensive study in probabilistic ....
Posted: Wed, 13 May 2020 06:42:20 GMT [source]
If only A is high then that combination is labeled with the small letter a. We began with the full model with all the terms included, both the main effects and all of the interactions. From here we were able to determine which effects were significant and should remain in the model and which effects were not significant and can be removed to form a simpler reduced model. The table above gives the data with the factors coded for each of the four combinations and below is a plot of the region of experimentation in two dimensions for this case. In these designs we will refer to the levels as high and low, +1 and -1, to denote the high and the low level of each factor.
The Pareto Plot
From the example above, a null outcome would exist if you received the same percentage of seizures occurring in patients with varying dose and age. The graphs below illustrate no change in the percentage of seizures for all factors, so you can conclude that the chance of suffering from a seizure is not affected by the dosage of the drug or the age of the patient. Regardless of whether the design is between subjects, within subjects, or mixed, the actual assignment of participants to conditions or orders of conditions is typically done randomly. An example graphical representation of a factorial design of experiment is provided in Figure 1 . As with any statistical experiment, the experimental runs in a factorial experiment should be randomized to reduce the impact that bias could have on the experimental results.
When the number of factors is large (typically more than about 5 factors, but this does vary by application), replication of the design can become operationally difficult. In these cases, it is common to only run a single replicate of the design, and to assume that factor interactions of more than a certain order (say, between three or more factors) are negligible. Under this assumption, estimates of such high order interactions are estimates of an exact zero, thus really an estimate of experimental error. As a further example, the effects of three input variables can be evaluated in eight experimental conditions shown as the corners of a cube. There are many simple examples of two independent variables being dependent on one another to produce an outcome.
A contrast in cell means is a linear combination of cell means in which the coefficients sum to 0. Contrasts are of interest in themselves, and are the building blocks by which main effects and interactions are defined. Treatment combinations are denoted by ordered pairs or, more generally, ordered tuples. The parentheses are often dropped, as shown in the accompanying table.
How To Add Biologics Manufacturing Efficiency With Design Of Experiments Part 2 - BioProcess Online
How To Add Biologics Manufacturing Efficiency With Design Of Experiments Part 2.
Posted: Wed, 05 Apr 2023 07:00:00 GMT [source]
In other words, the effect of wearing a shoe does not depend on wearing a hat. More formally, this means that the shoe and hat independent variables do not interact. It would mean that the effect of wearing a shoe on height would depend on wearing a hat. But in some other imaginary universe, it could mean, for example, that wearing a shoe adds 1 to your height when you do not wear a hat, but adds more than 1 inch (or less than 1 inch) when you do wear a hat. This thought experiment will be our entry point into discussing interactions. A take-home message before we begin is that some independent variables (like shoes and hats) do not interact; however, there are many other independent variables that do.
This can be conducted with or without replication, depending on its intended purpose and available resources. It will provide the effects of the three independent variables on the dependent variable and possible interactions. Having included all the terms back into a full model we have shown how to produce a normal plot. Remember that all of these effects are 1 degree of freedom contrasts of the original data, each one of these is a linear combination of the original observations, which are normally distributed with constant variance.
For example, a researcher might choose to treat cell phone use as a within-subjects factor by testing the same participants both while using a cell phone and while not using a cell phone. But they might choose to treat time of day as a between-subjects factor by testing each participant either during the day or during the night (perhaps because this only requires them to come in for testing once). Thus each participant in this mixed design would be tested in two of the four conditions. In the remainder of this section, we will focus on between-subjects factorial designs only. Also, regardless of the design, the actual assignment of participants to conditions is typically done randomly. In many factorial designs, one of the independent variables is a non-manipulated independent variable.
It is clear that in order to find the total factorial effects, you would have to find the main effects of the variable and then the coefficients. The additional complication is the fact that more than one trial/replication is required for accuracy, so this requires adding up each sub-effect (e.g adding up the three trials of a1b1). By adding up the coefficient effects with the sub-effects (multiply coefficient with sub-effect), a total factorial effect can be found. This value will determine if the factor has a significant effect on the outcome.
This combination of studies is similar in some respects to a factorial experiment but lacks certain unique advantages of factorial studies. The purpose of this commentary is to elaborate on those potential advantages of factorial studies, referring back to the article by Kaplan et al1 for context. The normal probability plot of the effects shows us that two of the factors A and C are both significant and none of the two-way interactions are significant.
These measures may be administered using specialized equipment or software. Blinding involves keeping participants, researchers, or both unaware of which treatment group participants are in, in order to reduce the risk of bias in the results. This involves randomly assigning participants to different groups or treatments to ensure that any observed differences between groups are due to the treatment and not to other factors. This design involves dividing participants into blocks based on a specific characteristic, such as age or gender, and then randomly assigning participants within each block to one of two or more treatment groups.

No comments:
Post a Comment